web好大一個洞
點閱數：1,229
下載數：87
點讚數：0
分享數：0
分享至：
web好大一個洞
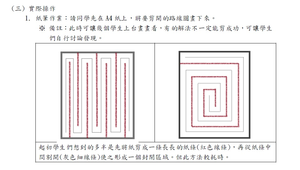
「一張A4大小的紙，能否剪一個洞，讓人可以穿越過去？」一個不經意聽到的問題，讓我興致勃勃的埋頭思考，腦中最初浮現的”不可能”，在我翻出書包中的廢紙實際操作之後逐漸瓦解，而成功的那一刻，當然是令人興奮不已的。
然而有趣的是，為什麼大家的腦中浮現的第一個念頭，都是”不可能”？我們到底是被什麼樣的框架限制著？為什麼竟跳脫不出A4大小的框框呢？筆者想到了7-11的藍色不織布小提籃，其實有異曲同工之妙，一個跳脫框架的小巧思，也許就能是一項偉大的發明，而我想讓學生學到的，就是別輕易地說”不可能”，不要小看自己，因為人有無限可能。
授權資訊
創用CC 姓名標示-非商業性 3.0 台灣
資源類型
教學設計
互動形式
混合式
領域
數學領域-數學
學習階段
國小1-2年級(一)
國小3-4年級(二)
國小5-6年級(三)
國中7-9年級(四)
國小3-4年級(二)
國小5-6年級(三)
國中7-9年級(四)
學習內容
D-2-1 分類與呈現：以操作活動為主。能蒐集、分類、記錄、呈現資料、生活物件或幾何形體。討論分類之中還可以再分類的情況。
R-4-4 數量模式與推理（II）：以操作活動為主。二維變化模式之觀察與推理，如二維數字圖之推理。奇數與偶數，及其加、減、乘模式。
D-6-2 解題：可能性。從統計圖表資料，回答可能性問題。機率前置經驗。「很有可能」、「很不可能」、「Ａ比Ｂ可能」。
D-9-3 古典機率：具有對稱性的情境下（銅板、骰子、撲克牌、抽球等）之機率；不具對稱性的物體（圖釘、圓錐、爻杯）之機率探究。
R-4-4 數量模式與推理（II）：以操作活動為主。二維變化模式之觀察與推理，如二維數字圖之推理。奇數與偶數，及其加、減、乘模式。
D-6-2 解題：可能性。從統計圖表資料，回答可能性問題。機率前置經驗。「很有可能」、「很不可能」、「Ａ比Ｂ可能」。
D-9-3 古典機率：具有對稱性的情境下（銅板、骰子、撲克牌、抽球等）之機率；不具對稱性的物體（圖釘、圓錐、爻杯）之機率探究。
學習表現
d-Ⅰ-1 認識分類的模式，能主動蒐集資料、分類，並做簡單的呈現與說明。
r-Ⅱ-2 認識一維及二維之數量模式，並能說明與簡單推理。
d-Ⅲ-2 能從資料或圖表的資料數據，解決關於「可能性」的簡單問題。
d-Ⅳ-2 理解機率的意義，能以機率表示不確定性和以樹狀圖分析所有的可能性，並能應用機率到簡單的日常生活情境解決問題。
r-Ⅱ-2 認識一維及二維之數量模式，並能說明與簡單推理。
d-Ⅲ-2 能從資料或圖表的資料數據，解決關於「可能性」的簡單問題。
d-Ⅳ-2 理解機率的意義，能以機率表示不確定性和以樹狀圖分析所有的可能性，並能應用機率到簡單的日常生活情境解決問題。
議題
閱讀素養教育
核心素養
A2 系統思考與解決問題
更新時間
2024-07-16
點閱數：1,229
下載數：87
點讚數：0
分享數：0
教學資源檔案連結
K9-TNC-CA-3055.pdf (255KB)
好大一個洞.pdf (84KB)
資源評論或心得分享