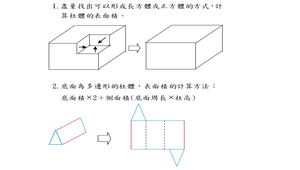
柱體的表面積雖然在本單元初次出現，但因為已經學習過基本平面圖形的面積算法與正方體、長方體的展開圖，所以應該不會有太大的困難。不過學生們很少有求正方體和長方體表面積的需要感，因此必須藉著在正方體和長方體表面塗色等操作活動來導入本單元的教學。 　　求柱體的表面積時，雖然可先計算每個面的面積，然後求其總和；但是柱體展開後，其整個側面成為一個長方形，底面一定是兩個全等的面，由此也可得出如下的算法： 　　側面積＝(底面的周長)×(柱體的高) 　　表面積＝(底面積)×2＋(側面積) 　　此種想法可適用於所有柱體(三角柱、四角柱、五角柱、六角柱、……)。 　　所謂立體實物或圖形的側面積是指上下兩個底面外的其餘部分的面積，就此而論，在本單元活動一的正方體與長方體亦有其側面積。但正方體的六個面都是一樣大小，因此其側面積恆為表面的六分之四，亦即四個面的面積之和；但長方體因其長、寬和高未必完全相等，側面積隨著放置的位置而改變。所以該活動教材均未提及側面積之計算，惟在日常生活中有關長方體側面的概念甚為普遍，如本單元練習的做做看就是很普通的實例。 表面積是一個極高層次的概念，遠超過本階段學生的認知程度，例如：在非平面性的立體上，表面積很難用平面區域的大小來思考；而到了不規則立體鐘，甚至連「表面」的概念都不容易建立，例如：一個有凹洞的球體，凹洞的內壁算不算是表面就很難定義。因此，本單元只是借用長方體的組成元素做一個數學內部的連結，並沒有要發展求算所有物體表面積的概念。