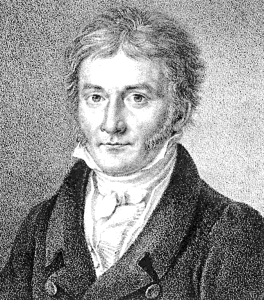
Lithograph from 1828, by Siegfried Detlev Bendixen, showing a portrait of the German mathematician Carl Friedrich Gauss at the age of 50. Source: http://commons.wikimedia.org/wiki/File:Bendixen_-_Carl_Friedrich_Gau ß,_1828.jpg. From en.wikipedia.org/wiki/Carl_Friedrich_Gauss: “Johann Carl Friedrich Gauss (/ɡaʊs/; German: Gauß, pronounced [ɡaʊs]; Latin: Carolus Fridericus Gauss) (30 April 1777 – 23 February 1855) was a German mathematician who contributed significantly to many fields, including number theory, algebra, statistics, analysis, differential geometry, geodesy, geophysics, mechanics, electrostatics, astronomy, matrix theory, and optics. Sometimes referred to as the Princeps mathematicorum (Latin, "the foremost of mathematicians") and "greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science and is ranked as one of history's most influential mathematicians.” Yes, he was all that and a lot more. But my favorite story is from his childhood. It is said one day his math teacher needed to do some work instead of teaching, so at the beginning of the lesson he told the pupils to add up the numbers from 1 to 100. They starting working and the teacher started doing whatever it was he needed to do. But just a few minutes later, young Karl raised his hand and said the numbers added up to 5050. The teacher just shook his head and told Karl not to fib. Closer to an hour later other pupils started raising their hands and they also said the result was 5050. The teacher then asked Karl how he could calculate the result so quickly. Karl said that 1+100=101, 2+99=101,3+98=101,...,50+51=101. There were fifty such pairs that added up to 101 each. Therefore, the sum of the numbers from 1 to 100 equals 50 times 101, and that is 5050. Duh! Whether the story is true or not, that is the basis of Gauss’ algorithm for adding any sequence of numbers starting anywhere and ending anywhere else. And it shows Gauss would make an amazing computer programmer because this type of problem solving is the heart of computer programming.
卡爾弗里德里希高斯
algebra、analysis、astronomy、blur、curve、differential、distribution、electrostatics、etc、Friedrich、Gauss、Gaussian、Gauß、geodesy、geometry、geophysics、German、Karl、mathematician、mathematics、matrix theory、mechanics、noise、number theory、optics、Princeps mathematicorum、Semi-Realistic People、statistics
代數、分析、天文學、模糊、曲線、微分、分配、靜電學、等等、弗里德里希、高斯、高斯、高斯、大地測量、幾何、地球物理、德語、卡爾、數學家、數學、矩陣理論、機械學、噪聲、數論、光學、高等數學、半現實的人、統計
資料來源：openclipart ( https://openclipart.org/ )